To understand what despeckling does, it is recommended that you read one of the guides to the Mandelbrot Set. Points are coloured based on their Dwell value.

The key to understanding despeckling is this: When we calculate the Dwell for each pixel in a picture, that pixel is not a point, but a square. The whole picture is divided up into a number of equally-sized squares. To calculate the Dwell for that pixel, we have to calculate the Dwell for the point that is in the centre of the square. Those centres are coloured red in the illustration below:

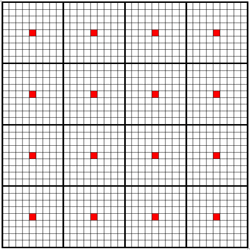
For low magnifications, this works fine. Problems occur at higher magnifications whereby the finished image can acquire a "speckly" appearance. Scattered about regions of the fractal are stray pixels that have inexplicably high Dwell values, and therefore have a colour that does not fit in with the surrounding colours. There are several causes for this speckling, but one of them is the chaotic nature of a fractal. Remember that fractal images exhibit infinitely fine detail; the more you enlarge, the more detail there is to discover. If the "red spot" at the centre of the pixel happens to be a point with a higher Dwell, the whole pixel will be skewed to have a higher Dwell. This has happened because of some very small detail within the pixel, but the result is that the Dwell calculated for the pixel is not representative of the points within it.

The solution is to calculate the Dwell for more than one point in each pixel, and then to average the Dwell values. For example, we could calculate a 2x2 grid of points - 4 points in total, such as those coloured blue in the illustration below:

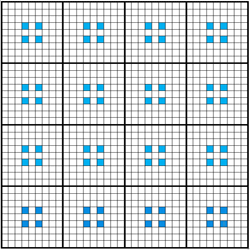
Alternatively, we could calculate a 3x3 grid of points - 9 points in total, such as those coloured green in the illustration below:

This feature is only available for Mandelbrot Fractals; in the Change Fractal Plugin, choose a despeckling level. "Off" means no despeckling is done. A level of 2 means a 2x2 grid is calculated (the blue dots above); a level of 3 means a 3x3 grid is calculated (the green dots above) and so on.

There is obviously a cost in time terms: The time taken to draw the fractal increases proportionally to the square of the despeckling level. The highest level allowed is 12, which would take 12x12 times, 144 times, as long to calculate as the same fractal without despeckling.

The other thing to bear in mind is that, as with smoothing, the resulting Dwell values may not be whole numbers.

The benefit of such despeckling can be seen in the examples below:

Despeckling Off
Level 2 Despeckle	Level 3 Despeckle
Level 4 Despeckle	Level 12 Despeckle

It can be seen that the biggest gain comes from moving from no despeckling to level 2; there is further improvement as the despeckling level is increased, but the increased computation time gives less and less benefit the more levels are added.